Cauchy Schwarz Inequality for Integrals
Assume that f x 0 for all x w w and f w f w 0. Let w 0 and let f.

Proof Of Cauchy Schwartz Inequality Mathematics Stack Exchange
The Cauchy-Schwarz inequality holds for much wider range of settings than just the two- or three-dimensional Euclidean space R2 or R3.

. How to prove integral inequality using Cauchy-Schwarz. First note that we have ww w2 1 w 2 2 w 2 n 0 for any w. Using the hint gave me a bit of trouble I think im doing something wrongtheres an easier way to do it.
Ab R such that fx2 is Riemann integrable on ab that is Z b a fx2 dx exists and is finite. That is tag4labeleq4 aibcdle Q_aibQ_cd and so one for the other derivatives. Cauchy-Schwarz Inequality for Integrals for any two functions clarification.
Yes if f is odd then certainly f2 is 0. I can prove the inequality using Riemann sums and the regular Cauchy-Schwarz inequality however I didnt see a way to prove that equality holds iff itex0int_ab f-λg2itex for some itexλinℝitex using this method. Do you see which.
Simply put m 2 m 2 and r 2 r 2 and we arrive at Cauchy Schwarz. Ad Browse Discover Thousands of Science Book Titles for Less. The set L2ab Definition The set L2ab is defined to be the set of functions f.
The Cauchy-Schwarz inequality also is important because it connects the notion of an inner product with the notion of length. Need help understanding the use of Cauchy-Schwarz inequality involving integrals. Begingroup Thanks for the help but I dont think this is correct.
Cauchy Schwarz Inequality Integral. I suppose we could assume this but if f and g have both even and odd components then both oddfoddg and evenfeveng terms will contribute to the integral on the LHS assuming there is more than 1 Grassmann variable of course. Show activity on this post.
Schwarzs inequality is sometimes also called the Cauchy-Schwarz inequality Gradshteyn and Ryzhik 2000 p. Verfication of deduction made using the Cauchy-Schwarz inequality. As such we say that Holders inequality generalizes Cauchy-Schwarz.
Note that it is almost a norm in the sense we have defined earlier in the course. Let a be the area under the graph of f bounded above the x-axis and let l be the length. Cauchy-Schwarz Inequality for Integrals for any two functions clarification.
If alpha is monotonically increasing on the set absubsetneq mathbb R let mathcalR_alphaa b denote the algebra of Riemann-Stieltjes integrable functions with respect to alpha. Speci cally uv jujjvjcos and cos 1. W w R be a continuous function that is piecewise continuously differentiable on w w.
Each of these terms however are still a part of the original space and hence still have a well-defined inner-product. We can also derive the Cauchy-Schwarz inequality from the more general Hölders inequality. Inequality for descents after applying Cauchy-Schwarz.
1099 or Buniakowsky inequality Hardy et al. For functions f L2ab the quantity kfk 2 sZ b a fx2 dx is called the L2-norm of f. Show activity on this post.
This means we can apply the Cauchy-Schwarz inequality directly to these derivatives as a means of screening the integrals. Cauchy-Schwarz Inequality for Integrals. Let and be any two real integrable functions in then Schwarzs inequality is given by.
Ad Publish Your Archaea Review Paper or Original Research Paper. 1 Written out explicitly. Hindawis Academic Journals Are Peer-Reviewed Open Access.
Science and technology Mathematics and Computer Science. Cauchy-Schwarz inequality for integrals in The Concise Oxford Dictionary of Mathematics. I like a lot the second one.
A2_607 Graphing reciprocal trigonometric functions. You know and love in R2 then the Cauchy-Schwartz inequality is a consequence of the law of cosines. If f x g x are real functions then f x g x dx 2 f x 2 dx g x 2 dx if all these integrals exist.
How to embed GeoGebra applets in revealjs slides. That is when frac a_i b_i biai is constant for all i i. 2 with equality iff with a constant.
In case you are nervous about using geometric intuition in hundreds of dimensions here is a direct proof. I know two beautiful direct proofs of this fact.
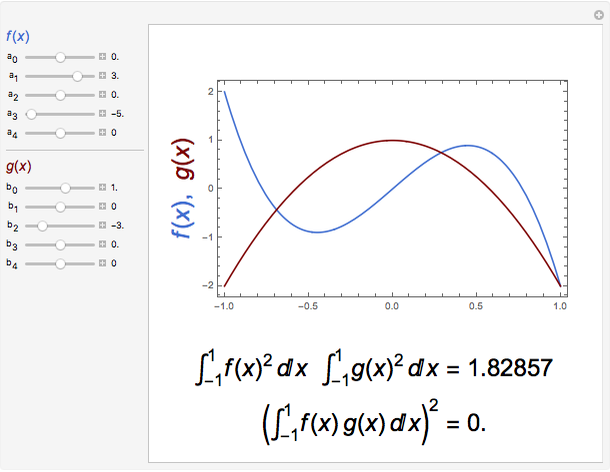
Cauchy Schwarz Inequality For Integrals Wolfram Demonstrations Project
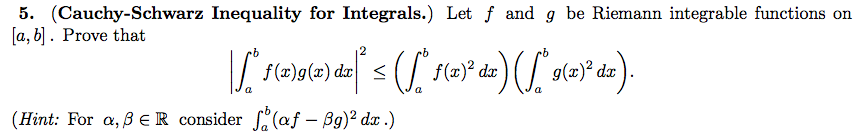
Cauchy Schwarz Inequality For Integrals Let F And Chegg Com

Solved 2 The Cauchy Schwarz Inequality For Integrals Chegg Com

Solved The Inequality Below Is Called Cauchy Schwarz Chegg Com

Real Analysis Question About Proof Of Showing Cauchy Schwarz Inequality Implies Schwarz Inequality From Spivak Mathematics Stack Exchange

Real Analysis Question About Proof Of Showing Cauchy Schwarz Inequality Implies Schwarz Inequality From Spivak Mathematics Stack Exchange
0 Response to "Cauchy Schwarz Inequality for Integrals"
Post a Comment